Binusian 2019

 

Stack:

• An important data structure which stores its elements in an ordered manner.
• Linear data structure which can be implemented using an array or linked list.
• Last In First Out (LIFO)
• 

Stack Operation:

• Push(x)         : add an item x to the top of the stack.
• Pop()  : remove an item from the top of the stack.
• Top()  : reveal/return the top item from the stack.

Array Representation:

• Top: Used to store topmost element of the stack
• Max: Used to store the maximum number of elements that the stack can hold.
• When Top is NULL, it means the stack is empty.
• When Top = Max – 1, it means the stack is full.

Linked List Representation:

• Linked list is more dynamic.
• One part of node stores data.
• One part of node stores the address of the next node.
• Top in linked list is the START pointer
• When Top is NULL, it means the stack empty.

Infix, Postfix, Prefix:

• Prefix notation, also known as Reverse Polish notation.
• Prefix : operator is written before operands
• Infix notation (commonly used)
• Infix  : operator is written between operands
• Postfix notation, also known as Polish notation.
• Postfix         : operator is written after operands
• 

Depth First Search

• An algorithm for traversing or searching in a tree or graph. We start at the root of the tree (or some arbitrary node in graph) and explore as far as possible along each branch before backtracking.
• 

Queue

• An important data structure which stores its elements in an ordered manner
• The elements in a queue are added at one end called the rear and removed from the other one end called front.
• FIRST IN FIRST OUT (FIFO)
• Two Variable in queue are Front and rear that point to the position where deletions and insertions can be done respectively.
• push(x)         : add an item x to the back of the queue.
• pop()  : remove an item from the front of the queue.
• front()         : reveal/return the most front item from the queue.
• 

Type Of Queue:

• Regular Queue
• Circular Queue
• Priority Queue

Priority Queue:

• An abstract data type in which the each element is assigned a priority.
• An element with higher priority is processes before an element with lower priority
• Two elements with same priority are processed on a first come first served (FCFS) basis

Breadth First Search

• An algorithm for traversing or searching in a tree or graph. We start at the root of the tree (or some arbitrary node in graph) and explore all neighboring nodes level per level until we find the goal.
• 

2 Maret 2016 kami kedatangkan Guest Lecturer bernama Bong Defendy yang juga merupakan alumni Bina Nusantara, Beliau adalah seorang TI profesional yang sudah berpengalaman di bidang TI.

Berikut rangkuman yang beliau sampaikan,
Big Data

adalah data dengan ciri berukuran sangat besar, sangat variatif, sangat cepat pertumbuhannya dan mungkin tidak terstruktur yang perlu diolah khusus dengan teknologi inovatif sehingga mendapatkan informasi yang mendalam dan dapat membantu pengambilan keputusan yang lebih baik

Arduino
adalah sebuah platform open source (sumber terbuka) yang digunakan untuk membuat proyek-proyek elektronika.
Raspberry Pi
sering juga disingkat dengan nama Raspi, adalah komputer papan tunggal (Single Board Circuit /SBC)yang memiliki ukuran sebesar kartu kredit. Raspberry Pi bisa digunakan untuk berbagai keperluan, seperti spreadsheet, game, bahkan bisa digunakan sebagai media player karena kemampuannya dalam memutar video high definition
Latex

adalah bahasa markup atau sistem penyiapan dokumen untuk peranti lunak TeX. Tex merupakan program komputer yang digunakan untuk membuat typesetting suatu dokumen, atau membuat formula matematika
Cloud Storage
Cloud Storage adalah sebuah teknologi penyimpanan data digital yang memanfaatkan adanya server virtual sebagai media penyimpanan.
Augmented Reality
Augmented Reality teknologi yang menggabungkan benda maya dua dimensi dan ataupun tiga dimensi ke dalam sebuah lingkungan nyata tiga dimensi lalu memproyeksikan benda-benda maya tersebut dalam waktu nyata. Tidak seperti realitas maya yang sepenuhnya menggantikan kenyataan, realitas tertambah sekadar menambahkan atau melengkapi kenyataan.
SASS (Syntactically Awesome Stylesheets)
Sass (Syntactically Awesome Stylesheets) adalah sebuah pengembangan dari CSS3 dengan menambahkan nested rules, variables, mixins, selector inheritance, dan banyak lagi. Dia menerjemahkan CSS dengan struktur yang lebih baik

Dalam istilah ilmu komputer, sebuah struktur data adalah cara penyimpanan, penyusunan dan pengaturan data di dalam media penyimpanan komputer sehingga data tersebut dapat digunakan secara efisien.

Dalam teknik pemrograman, struktur data berarti tata letak data yang berisi kolom-kolom data, baik itu kolom yang tampak oleh pengguna (user) atau pun kolom yang hanya digunakan untuk keperluan pemrograman yang tidak tampak oleh pengguna. Setiap baris dari kumpulan kolom-kolom tersebut dinamakan catatan (record). Lebar kolom untuk data dapat berubah dan bervariasi. Ada kolom yang lebarnya berubah secara dinamis sesuai masukan dari pengguna, dan juga ada kolom yang lebarnya tetap. Dengan sifatnya ini, sebuah struktur data dapat diterapkan untuk pengolahan database (misalnya untuk keperluan data keuangan) atau untuk pengolah kata (word processor) yang kolomnya berubah secara dinamis. Contoh struktur data dapat dilihat pada berkas-berkas lembar-sebar (spreadsheet), pangkal-data (database), pengolahan kata, citra yang dipampat (dikompres), juga pemampatan berkas dengan teknik tertentu yang memanfaatkan struktur data

Struktur data terdiri dari:

1. Static memory allocation (array)
2. Dynamic memory allocation (linier dan non linier)

Contoh struktur data yang biasa digunakan:

Array

Linked list

Queue

Stacks

binary tree

• ARRAY

-bersifat homogen (memilki tipe data yang sama)

-merupakan kumpulan data yang sejenis

-bisa diakses dengan mudah (contoh: nama[1])

-indeksnya dimulai dari nol “0”

-array juga memiliki alamat yang saling bersebelahan

 

• Array Satu Dimensi seperti halnya variabel biasa, array juga harus didefinisikan sebelum ia dapat digunakan. Untuk mendefinisikan array : TipeData namaArray [ukuran]; Contoh : string namaPemain[9]; Perlu diingat bahwa ukuran array adalah max index + 1. Hal ini dikarenakan index selalu dimulai dari nol.
• Array Dua Dimensi, Array dapat dibuat berdimensi dua, dimana array ini mempunyai dua buah index / subscript. Sama seperti array dimensi satu, array dua dimensi juga merupakan kumpulan elemen-elemen yang bertipe data sama dengan satu nama variabel, tetapi terdiri dari dua index. Contoh : int posisi [3][4]; int tipe data array posisi variabel, nama array [3] index (menyatakan jumlah baris) [4] index (menyatakan jumlah kolom)

Storing Array Values

• Initialization of Arrays

Contoh:  int marks[5] = {90, 82, 78, 95, 88};

• Inputting Values

Contoh:  int i, marks[10];

for (i=0; i<10; i++)

scanf(“%d”, &marks[i]);

• Assigning Values

Contoh:  int i, arr1[10], arr2[10];

for(i=0; i<10; i++)

arr2[i] = arr1[i];

Operations in Array

• Traversal
• Insertion
• Searching
• Deletion
• Merging
• Sorting

• Pointer

Pointer adalah sebuah variabel yang menyimpan alamat dari variabel lain.

Terdiri dari 2 operators penting di pointer adalah:

• & the address operator
• * the dereferencing operator

• Linked list

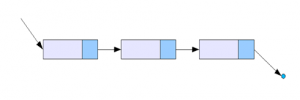
Linked list adalah sejumlah simpul (node) yang dikaitkan dengan simpul yang lain dengan bantuan pointer dalam suatu urutan tertentu. Suatu linked list dikatakan single linked listapabila hanya ada satu pointer yang menghubungkan setiap node (satu arah “next”).

• Queue

 

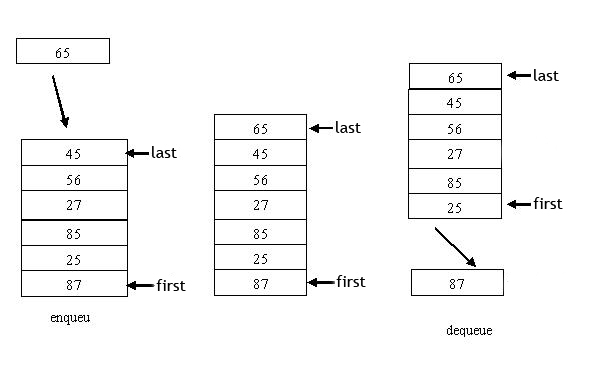
Queue / Antrian adalah suatu kumpulan data yang mana penambahan elemen hanya bisa dilakukan pada satu ujung (disebut dengan sisi belakang atau tail/rear) dan penghapusan atau pengambilan elemen dilakukan lewat ujung lain (disebut dengan sisi depan atau head/front). Antrian menggunakan prinsip Pertama Masuk Pertama Keluar – First In First Out (FIFO). Dengan kata lain urutan masuk sama dengan urutan keluar. Antrian banyak dijumpai dalam kehidupan sehari-hari. Mobil-mobil yang mengantri digerbang tol untuk membeli karcis tol; orang-orang yang mengantri di loket untuk membeli karcis film juga membentuk antrian. Elemen yang pertama kali masuk ke antrian akan keluar pertama kalinya. DEQUEUE adalah mengeluarkan satu elemen dari suatu antrian. Terdapat satu buah pintu masuk di suatu ujung dan satu buah pintu keluar di ujung satunya sehingga membutuhkan variabel Head dan Tail.

• Stack

 

Stack dapat diartikan sebagai tumpukan dari benda atau data yang seolah-olah diletakkan di atas data yang lain dimana data yang pertama kali masuk akan terakhir. Secara sederhana sebuah stack bisa digambarkan sebagai tumpukan buku yang disimpan dengan cara ditumpuk keatas. Dimana buku yang pertama kali disimpan atau ditumpuk ada di paling bawah dan yang selanjutnya ditumpuk diatasnya. Dan ketika kita melakukan pengambilan buku ototmatis buku yang terkahir ditumpuk atau disimpan terakhir akan mejadi yang pertama diambil, istilah ini kemudian disebut FILO (First In Last Out) dan bertambah atau berkurangnya data melalui satu ujung yang sama yaitu ujung atas tumpukan (Top of Stack).

• Binary Tree

 

Dalam ilmu komputer, sebuah pohon biner (binary tree) adalah sebuah pohon struktur data di mana setiap simpul memiliki paling banyak dua anak. Secara khusus anaknya dinamakan kiridan kanan. Penggunaan secara umum pohon biner adalah Pohon biner terurut, yang lainnnya adalah heap biner.